¶树结构
¶概念解释:
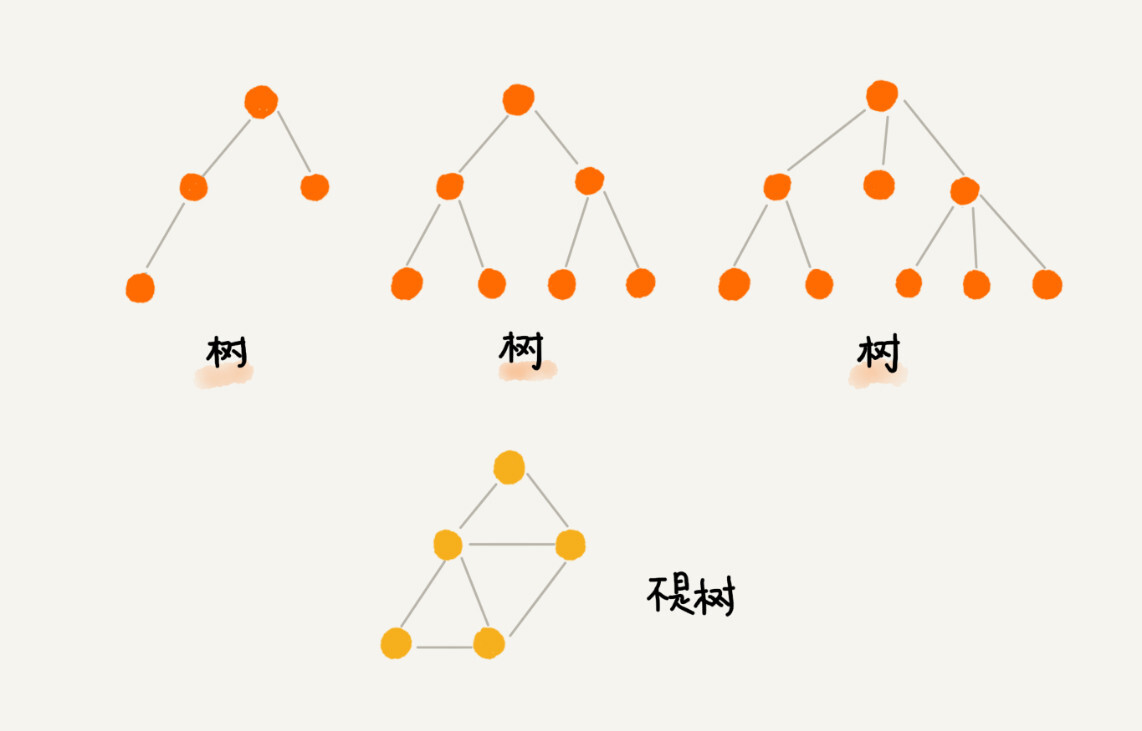
树的结构和现实中的树是类似的:具备根,枝干,叶子等,只不过在树结构中,这些被对应转换成了根节点,节点之间的边以及子节点这些概念,用图来展示会比较直观:
图中这种由一个根节点向下延申出来子节点,然后子节点继续向下延申直到没有节点,且每个节点的同一层节点没有直接联系,这种结构就是树
¶二叉树
树的结构中最常用的还是二叉树,指的是每个节点最多具备两个分叉(子节点)的树结构,但并不意味着必须左右子节点都具备
在二叉树中又有比较特殊的结构:
满二叉树:除叶子节点外,所有的节点都具备左右子节点的树结构
完全二叉树:最后一层节点靠左,且除最后一层外其他层数节点个数达到最大,如下图:
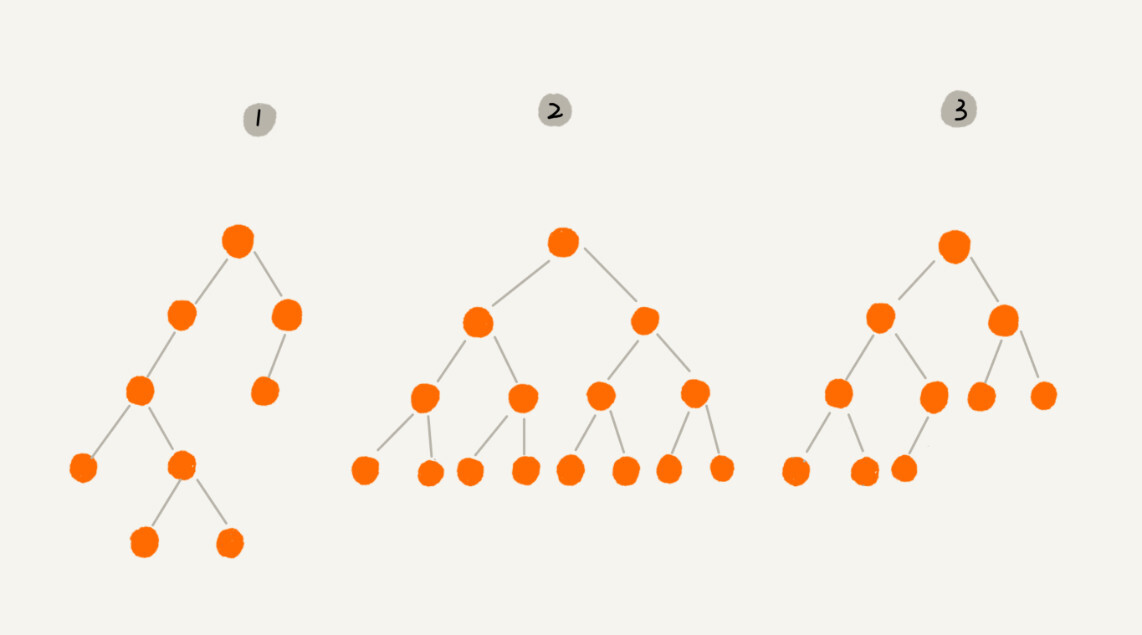
编号2为满二叉树,编号3则是符合完全二叉树的定义
¶树结构的表示:
- 有了上面的这些概念展示,比较容易想到的表示树的方式是链表:每个节点存储本身的值和指向左右节点的引用,标准的树结构
- 除此之外还有基于数组的顺序存储,前面的二叉树中完全二叉树的概念被区分开来也许会让人觉得多余,但这是和树的存储方式有关的
- 假设给出数组:{1,2,3,4,5,6,7,8,9},按照顺序将 1 作为根节点存储在下标为 1 的位置,2,3作为1的左右子节点存储在下标为 2,3 的位置,而 2 的字节点 4,5存储在下标为 4,5的位置 ,可以得出当以下标1作为起始位置存储 , 在一棵完全二叉树中,i 位置的节点的子节点的存储位置可以表示成 : 2*i , 2*i +1;
- 如果树的结构是一棵完全二叉树,以数组的方式存储会比链式存储节省存储的引用的空间,要求最后一层子节点靠左也是为了符合数组需要连续内存空间的的存储特性
¶树的遍历:
树的常见遍历方式有三种:
- 前序遍历:先遍历节点本身,再顺序遍历左右节点,简单记忆为:上左右
- 中序遍历:先遍历左子节点,再遍历父节点,最后右子节点,记忆为:左上右
- 后序遍历:先顺序遍历左右子节点,然后是根节点,记忆为:左右上
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
//树结构
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
//前序遍历
public static void frontTraverse(TreeNode root){
if(null == root){
return;
}
System.out.print(root.val + " ");
frontTraverse(root.left);
frontTraverse(root.right);
}
//中序遍历
public static void middleTraverse(TreeNode root){
if(null == root){
return;
}
frontTraverse(root.left);
System.out.print(root.val + " ");
frontTraverse(root.right);
}
//后序遍历
public static void backTraverse(TreeNode root){
if(null == root){
return;
}
frontTraverse(root.left);
frontTraverse(root.right);
System.out.print(root.val + " ");
}思路对了就比较容易实现
¶二叉查找树:
概念:
二叉查找树是二叉树的一种常用类型,它的结构特点是:树的任意一个节点,其左子数任意节点的值都小于这个节点的值,右子树任意节点的值都大于这个节点的值;由这个特性不难联想到,在一棵二叉搜索树中查找一个元素只需要遍历其中一半的节点
而且根据树本身的存储结构,查找元素的方法可以很容易地实现成递归方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//树结构
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
/**
* 在一颗二叉查找树中定位元素
*/
public TreeNode getNodeInSearchTree(TreeNode root,int value){
if(null == root){
return null;
}
if(root.val == value){
return root;
}else if(root.val < value){
getNodeInSearchTree(root.right,value);
}else{
getNodeInSearchTree(root.left,value);
}
return null;
}看了下别人的实现,用while循环就可以实现了,可以不用递归
插入节点的思路也类似,都是要先定位可以插入的位置:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
* 在一颗二叉查找树中插入元素
*/
public TreeNode insertTreeNode(TreeNode root,int value){
if(null == root){
root = new TreeNode(value);
return root;
}else if(value > root.val){
//如果插入值大于当前节点的值,判断是否有右子树
if(null == root.right){
TreeNode right = new TreeNode(value);
root.right = right;
return right;
}else{
insertTreeNode(root.right,value);
}
}else{
//同理
if(null == root.left){
TreeNode left = new TreeNode(value);
root.left=left;
return left;
}else{
insertTreeNode(root.left,value);
}
}
return null;
}查找插入位置的代码和单纯定位元素很类似,以上两个操作都相对比较容易理解和实现,删除操作就不一样了
删除二叉搜索树中的某个节点,需要依旧维持它的特性不变,需要考虑的情况有三种:
- 删除根节点
- 删除带有单个子节点的节点
- 删除带有两个子节点的节点,这种情况是最复杂的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64//二叉搜索树删除指定节点
//树结构
static class TreeNode {
int val;
TreeNode parent;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
TreeNode(int val, TreeNode left, TreeNode right,TreeNode parent) {
this.val = val;
this.left = left;
this.right = right;
this.parent = parent;
}
}
/**
* 在树中删除节点
*/
public static void delTreeNode(TreeNode root,int value){
if(null == root){
return;
}else if(value > root.val){
delTreeNode(root.right,value);
}else if(value < root.val){
delTreeNode(root.left,value);
}else if(root.val == value){
//删除根节点,分为三种情况,没有左子节点,没有右子节点,两者都有
if(root.left == null && null != root.right){
root = root.right;
return;
}else if(root.left !=null && root.right == null){
root = root.left;
return;
}else{
//左右子节点都存在的情况下,将右子树中的最左节点作为根节点
//因为它是删除根节点后,符合大于左子树节点,小于右子树节点的节点
TreeNode right = root.right;
TreeNode temp = right.left;
while(temp.left !=null){
temp=temp.left;
}
TreeNode pa = temp.parent;
pa.left = null;
temp.parent=null;
root.val = temp.val;
return;
}
}
}实现的时候发现树结构缺少了 parent 属性,无法删除父节点和它之间的关联
其实在删除带有两个子节点的节点的场景中,就是将右子树的最小节点的值替换到根节点,然后删除该节点的引用,这样转换一下,思路就简单很多
- 二叉查找树的其他特性:
- 对于一颗符合条件的二叉查找树来说,我们前面实现的中序遍历,刚好可以根据二叉查找树的特点,按照顺序输出它的所有节点
- 存储重复数据:
- 通常数据结构会用来存储对象数据,将对象的某些属性作为 key , 也就会存在可能两个对象使用了一样的key,对于这种情况,二叉查找树可以允许存储重复数据( 重复键 ),有两种方式实现:
- 树的节点使用其他数据结构(链表,数组)存储相同的key,类似于散列冲突的解决方案;
- 每个节点之存储单个数据,当存储下一个相同的key,作为该节点的右子节点存储;这种方式存储也意味着需要改变遍历树的方式,通过重复键索引的时候,需要一直遍历符合条件的键的右子树,直到遍历出所有符合条件的键值
- 第一种方式比较熟悉也比较简单,遍历指定的key定位到某一个节点后,再遍历该节点的链表/数组就可以得到对象;第二种方式就得循环遍历该节点的右子树直到叶子节点为止
- 通常数据结构会用来存储对象数据,将对象的某些属性作为 key , 也就会存在可能两个对象使用了一样的key,对于这种情况,二叉查找树可以允许存储重复数据( 重复键 ),有两种方式实现:
- 二叉查找树的时间复杂度分析:
- 我们知道树的时间复杂度和树的高度有关,而一棵平衡二叉树是完全二叉树,除最后一层外,就是满二叉树,假设 K 层的二叉查找树,从上到下依次有 : 1,2,4,8,16 … 2 ^(K-2) + x 个节点 , 最后那个 x 代表最后一层的节点个数,范围是 1 ~ 2(K-1) 之间
- 则一棵 K 层的二叉查找树,总节点个数为:2^0 + 2^1 + 2^2 + … + 2^(k-2) + x = 2^(k-2) -1 + x = [2^(k-2) +1,2^(k-1)] ,总结点数用 n 表示的话,层数 K 和 n 的关系可以近似表示为 : K = log2n ,而时间复杂度计算我们可以考虑忽略常数,因此一颗二叉查找树的高度接近 logn ,对于插入,删除的时间复杂度为O(logn)的对数阶
- 二叉树和散列表的对比:
- 散列表存储的数据一般是无序的,只需要满足快速存取,想要有序输出得额外排序;而二叉查找树插入性能和散列类似,有序输出树中节点的话只需要中序遍历
- 散列表不可避免地需要考虑扩容的问题,扩容的成本随着已存储的节点数而增加,散列频繁冲突的情况下,性能会退化;而二叉树中的平衡二叉查找树(例如红黑树)的性能十分稳定,因为它会根据节点插入情况进行左右旋转来维持自身的二叉查找树和平衡树的特性,维持高效的操作(不过频繁的左右旋似乎也会导致性能开销?)
- 设计一个优良的散列表需要考虑:散列函数,扩容方案以及缩容方案等;而维持一棵平衡二叉查找树只需要考虑如何在节点插入后维持树的平衡特性,相比之下后者有比较成熟稳定的实现方案(红黑树)
¶小结:
二叉查找树的特点是:节点的左子树节点都小于该节点,节点的右子树节点都大于该节点;这个特点对于节点的遍历操作十分友好而且高效;
二叉查找树本身可能因为节点的插入或者删除操作仅发生在左子树或者右子树而导致自身的结构退化,丧失高效的性能;但是一棵平衡二叉查找树会在每次插入或者删除节点后,进行平衡操作,得以继续维持O(logn)级别的操作时间复杂度
求一棵树的高度:
1
2
3
4
5
6
7
8
9
10
public static int treeHigh(TreeNode root){
if(null == root){
return 0;
}else {
return 1 + Math.max(treeHigh(root.left),treeHigh(root.right));
}
}